- A+
《The Mathematics of Poker》中文翻译
 感谢梅有钱(梅老板)的合作翻译(这一篇是我自己翻的嘿嘿嘿~~~~~)
感谢梅有钱(梅老板)的合作翻译(这一篇是我自己翻的嘿嘿嘿~~~~~)
牌例13.1-AKQ游戏#1
一条半街。
底池大小为2个下注单位。
限制的下注大小为1个下注单位。
完整的摊牌前收益矩阵(从Y玩家的视角)如下图所示:
我们的目标是找到这个游戏的最优策略。那我们先可以通过去除劣势策略来简化这个游戏。对比当X玩家拿到A时的所有选项,我们会发现在任何情况下跟注都是比弃牌有更高的期望收益的。也就是说相比跟注,弃掉A是被统治的(占劣势的)。因此我们可以将X玩家手持A并且弃牌这一选项直接去除,既然这个选项是被跟注统治的话。同理,我们也可以发现用Q跟注是被用Q弃牌这个选项统治的。因此我们也可以将X玩家手持Q并且跟注移除出我们的策略选项,因此得到一个简化的游戏:
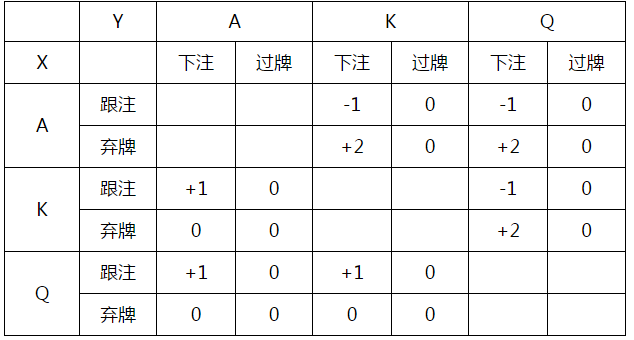
现在我们可以把重点放到Y的那些劣势策略。我们可以发现拿着K下注是被拿着K过牌统治的,同理拿着A过牌也是被拿着A下注统治的。因此我们可以通过去除这些策略选项来进一步简化游戏:
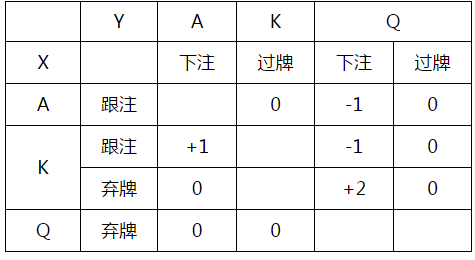
现在我们想想通过直觉能得到些什么。首先考虑一下X的策略选项。我们发现有两个策略是X一定会执行的:拿A下注和拿Q弃牌。这是比较显然的,我们既不会在河牌拿着坚果牌时面对一个下注弃牌,也不会拿着没用任何希望获胜的牌去跟注一个下注。既然X永远不会做出这些决策,那我们显然可以将它们从游戏决策中去除。
接下来,面对一个简化过的游戏,我们用同样的方式去考量Y的策略选项。如果Y拿着K,他知道他的下注永远不会让X的A弃牌,并且永远不会得到X的Q的跟注。而当他拿着A时,他的下注永远不会亏损,并且偶尔会得到一些对手的K的跟注。
通过消去劣势策略,我们得到了一个更加简练的游戏——事实上,从一个策略选择的角度来看,这个游戏就是一个2*2的矩阵,就像我们在之前的章节进行过的游戏一样。这里我们可以从一个纯粹的角度来看策略的变化,像我们之前描述的那样。
如果X拿着K时总是跟注,Y的最优应对是从不诈唬并且只做价值下注。作为应对,X对于这个策略应该弃掉所有的K。而Y又可以通过一直诈唬(拿到Q时)来剥削X;那么X又可以回到最初的用所有K跟注的策略。这意味着这个游戏有一个混合策略的纳什均衡。
我们实际上可以通过定义未被统治的策略互相间的权益来构建一个2*2的矩阵:
两个未被统治的策略选项是Y是否选择用Q诈唬,和X是否选择用K跟注。
我们通过考虑X可能持有的手牌以及受益来定义Y的两个选项的权益。
我们将四个策略选项如下命名:
r1:Y用Q诈唬;
r2:Y用Q过牌;
x1:X用K跟注;
x2:X用K弃牌。
我们可以得出这些策略互相对阵的期望收益:
r1 vs x1:
当Y有A时,他可以从X的K上拿到额外的价值,而无法从X的Q上获取。当Y有K时,不会有任何下注。当Y有Q时,他会选择诈唬,并且输给X的A和K。
每一种对阵都会以1/6的概率出现,Y在一种对阵中收获一个下注,另两种对阵中损失一个下注,因此总共的期望为:
<r1,x1>=-1/6
r2vs x1:
当Y有A时,他可以从X的K上拿到额外的价值,而无法从X的Q上获取。当Y有K时,不会有任何下注。当Y有Q时,不会有任何下注
Y在一种对阵中收获一个下注,任何对阵中都不会出现亏损,因此总共的期望为:
<r2,x1>=+1/6
r2 vs x2:
当Y有A时,他无法获取任何价值(X永远弃牌)。当Y有K时,不会有任何下注。当Y有Q时,他会选择诈唬,在X有A时损失一个大盲,在X有K时额外收获两个大盲。
Y在一种对阵中收获两个大盲,另一个对阵中损失一个下注,因此总共的期望为:
<r1,x2>=+1/6
r2vs x2:
当Y有A时,他无法获取任何价值。当Y有K时,不会有任何下注。当Y有Q时,不会有任何下注,因此对期望收益没有任何净影响。
<r2,x2>=0
我们可以从下表的这个2*2矩阵中看到博弈结果:

将矩阵中的每一个方格同时乘以一个正数并不会对博弈的策略产生任何的影响。而如果乘以-1会让双方的收益对换。
如果我们将整个AKQ游戏#1乘以-6,我们可以得到:

对于读者来说这个矩阵与之前第十章的有点类似;回忆一下警察与强盗游戏的收益矩阵:

这个游戏与警察与强盗游戏是完全一致的。从之前的游戏的分析我们知道最优策略是(1/3,1/3),并且我们可以对比这个结果与我们之后直接得到的结果。
我们也可以通过找到每一个玩家让对手两个策略选项无差异的策略来解决这个游戏。考虑Y,他必须选择是否用Q去诈唬。他的两种行动的摊牌前EV分别是(c代表X用K跟注的频率):
<Y,诈唬>=(输给A)+(输给K)+(K弃牌,赢得底池)
<Y,诈唬>=p(X有A)(损失一个大盲)+p(X有K)p(X跟注)(损失一个大盲)+p(X有K)p(X弃牌)(底池)
<Y,诈唬>=(1/2)(-1)+(1/2)(c)(-1)+(1/2)(1-c)(2)
<Y,诈唬>=(1/2)(-1)+(1/2)[(c)(-1)+(1-c)(2)]
<Y,诈唬>=-1/2-1/2c(-1)+1-c
<Y,诈唬>=1/2-3/2c
<Y,过牌>=0
为了让着两个期望值相等:
0=1/2-3/2c
C=1/3
接下来,让X拿到K时跟注与弃牌是无差异的。用b表示Y用Q诈唬的频率:
<X,跟注>=(输给A)+(赢下Q)
<X,跟注>=1/2(-1)+1/2[b(1)]
<X,跟注>=-1/2+1/2b
<X,弃牌>=1/2(b)(-2)
<X,弃牌>=-b
-1/2+1/2b=-b
b=1/3
因此我们得到了最优策略组合:X应该在拿到K时在1/3的时候跟注,而Y应该在拿到Q时在1/3的时候诈唬。


举报
+1
以上文章来源于网络,由6up扑克之星中文网整理发布