- A+
《The Mathematics of Poker》中文翻译
 感谢梅有钱(梅老板)的合作翻译(这一篇是我自己翻的嘿嘿嘿~~~~~)
感谢梅有钱(梅老板)的合作翻译(这一篇是我自己翻的嘿嘿嘿~~~~~)
我们再次在这里用直觉思考下这里发生了什么。Y的思路是从他的手牌范围内通过下注获取价值。从一个剥削的角度来看,如果他准确地知道X在拿到K时如何决策,他就可以根据这个来决定是否诈唬。然而,如果说他不知道X如何决策,或者说他不管对手如何决策都希望获取最大的价值。
对于他来说有两种意义的价值:用Q偷取底池,或者在拿到A时获得支付。因此他希望创造一种两个选项获取的价值相当的情形。那么他的对手就没有办法来剥削他了。那么他应该做的,就是以一定的频率去诈唬使得他的对手无论怎么做,他的总体策略的价值是不变的;具体的说,就是无论对手是否用K跟注。结果显示在这种情况下,合理的A与Q诈唬的搭配比例是3:1;也就是说他会用1/3的Q做下注,既然他会用所有的A下注的话。回忆一下章节11,我们称诈唬的频率为ɑ,并且显示这个下注的价值为1/(P+1)(见等式11.1)。而对于一个两倍底池的下注,我们可以确实计算出这个比例为1/3。
对X来说也是同样的道理。他希望跟注的足够多使得对手用Q诈唬与否是无差异的。当他的对手诈唬成功时,他获得了两个大盲,而他诈唬失败时仅仅损失一个大盲。因此X每弃牌一次就必须跟注两次使得对手的诈唬是无差异的。这个数值应该为2/3(剩下1/3的情况弃牌)。但是在对手诈唬的一半的情况下,X手持A。因此他需要额外跟注的频率为2/3-1/2,即1/6。既然在对手拿到Q的情况下X有1/2的可能性拿到K,那么他必须跟注2/6或者说1/3比例的K。再次回忆一下章节11,我们推断出X会在ɑ的情况下弃掉一手可以击败诈唬的牌。与之前一样,他这里会在1/3的情况下弃掉比对手的诈唬好的牌。
就像你预计的一样,Y在这个游戏中可以获得价值;毕竟,他可以在所有情况下随后过牌来获得0ev,那么下注和诈唬显然对他来说是有利可图的。我们可以通过整合策略与收益来计算出Y在这个游戏中的价值。我们可以计算每个行动所有可能的概率情况,但其实我们可以走一条捷径。回忆一下当一个玩家采用最优策略的时候,X跟注与弃牌是无差异的;也就是说,他跟注与弃牌的收益是相等的。那我们可以简单地假设他每次都弃牌。当然他如果真的每次都弃牌,他的策略是可剥削的了。但是我们既然只是为了计算整个游戏的收益情况而不是策略情况,我们可以简单地调整Y的策略集。
那么Y在这个游戏中的价值恰好为1/18个大盲。我们邀请读者来判定这是否是X无论拿到K时用什么样的策略来跟注都会有这样的期望收益。
我们现在可以来解决这个一条半街的游戏,找到了一个固定底池大小的最优策略(两个大盲)——然而,我们可以用相同的方式方法去探索解决任意大小的底池。如果我们假设底池大小未不固定的P,我们可以轻松地解决AKQ游戏#2。
牌例13.2——AKQ游戏#2
一条半街。
底池大小为P个单位。
限定下注大小为1个单位。
再次地,我们可以得到完整的收益矩阵:
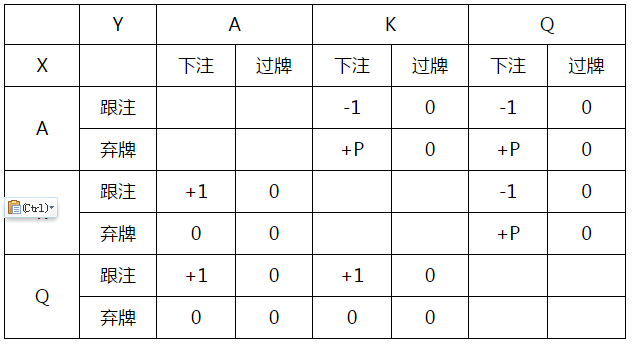
这个矩阵可以通过剔除劣势策略来简化,就如同AKQ游戏#1中的一样(牌例13.1),因此有:
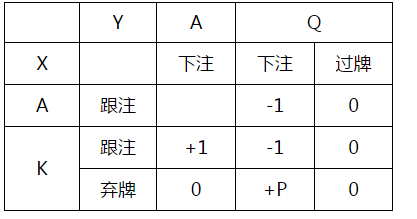
我们的两个无差异等式应如下修正(假设b是Y用Q诈唬的频率,c是X用K跟注的频率):
<Y,诈唬>=(输给A)+(输给K)+(K弃牌,赢得底池)
<Y,诈唬>=(1/2)(-1)+(1/2)(c)(-1)+(1/2)(1-c)(P)
<Y,诈唬>=(1/2)(-1)+(1/2)[(c)(-1)+(1-c)(P)]
<Y,诈唬>=-1/2-1/2c+1/2P-1/2Pc
<Y,过牌>=0
为了让这两个数值相等:
-1/2-1/2c+1/2P-1/2Pc=0
1+c-P+Pc=0
(P+1)c=P-1
c=(P-1)/(P+1)
这个c的取值是X用K跟注的频率。当Y持有Q时,X有一半的可能性有A,一半的可能性有K。因此他总体手牌组合(A和K)的跟注频率是1/2+(1/2)(P-1)/(P+1)。这也意味着他要在1/(P+1)的时候弃牌,或者用熟悉的常量ɑ,在他的手牌中,为了使得Y是否诈唬是无差异的。
用类似的方法,我们有:
<X,跟注>=(输给A)+(赢下Q)
<X,跟注>=1/2(-1)+1/2[b(1)]
<X,跟注>=-1/2+1/2b
<X,弃牌>=1/2(b)(-P)
再次地,我们让这两个数值相等:
-1/2+1/2b=1/2(b)(-P)
-1+b=-bp
b(1+P)=1
b=1/(1+P)
b=ɑ
并且再次地,我们发现这里Y应该诈唬的频率也必须是ɑ。
我们也可以很快地计算出Y在这个游戏中的期望收益:
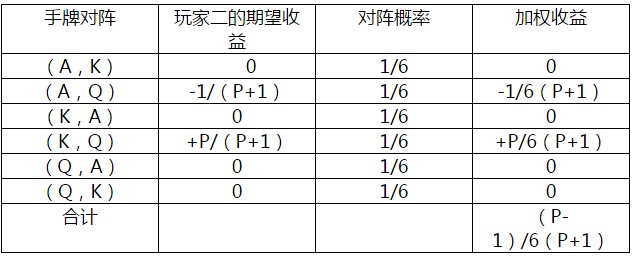
因此这个游戏对于Y的总期望收益为(P-1)/6(P+1)。我们可以发现当底池大小趋向于无穷的时候,Y的期望收益趋向于1/6。如果底池非常大的的时候,那么X几乎会用他所有的K去跟注,并且Y几乎永远不会诈唬,也就使得当Y拿到A而X拿到K时可以拿到所有价值。这种情况会在1/6的情况下发生。
而一个额外的条件必须被满足:以上的推论仅仅在底池大小大于1时才是有效的。原因是如果底池大小小于1,那么Y用Q诈唬是在烧钱——X会跟注所有的A,也就是他所持手牌的一半。既然Y在X的K弃牌时收获一个底池,而当X有A时损失一整个下注,那么诈唬总是亏钱的,即使X的所有K都弃牌的话。那么整个游戏在这个阶段发生了改变。当底池从大到小逼近1的时候,诈唬频率越来越高——当底池为2时,频率为1/3,底池为1.5时,频率为2/5,底池为1.1时,频率为10/11。而当底池恰好为1的时候,Y停止了诈唬。
我们也可以用一张图像来观察游戏的期望值随底池大小变化的情况。注意在底池P=1的时候图像有一个突然的变化;Y从从来不诈唬转变为诈唬手牌中的一半。这变化产生的原因是跟注突然变成了一个混合策略,而诈唬也是。在这个尺寸以下的底池大小,没有任何一边会选择诈唬或者跟注;这是不可被剥削的因为对手手牌范围中A的比例被限定了。我们也会发现在一些底池很大的情况下X必须频繁跟注,而Y并不用那么频繁地诈唬,因此,当底池大小越大时,游戏对Y越有利。
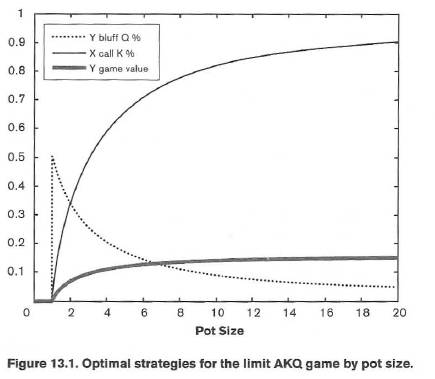
这里我们了解到的一个重要内容是底池大小的变化会影响两位玩家的策略和权益;而解决特定底池大小的问题通常与解决不定底池大小的问题同样轻松。在之后,除非真的有必要,否则我们会总体放弃讨论特定底池大小的游戏,而我们会更倾向于去讨论不定底池大小P的问题。
举报
+1
以上文章来源于网络,由6up扑克之星中文网整理发布